Introduction:
Students who are ready for Algebra 2 have successfully completed Algebra 1.Preparing for the Assessment:
You will need the following items:
- paper
- pencil with eraser
Students may also use a calculator to complete this assessment.
Gather these materials before you begin.
Student Portion:
Print out a copy of the Algebra 2 Readiness Assessment. The printed part of the assessment is to be completed independently by the student and should take approximately 45 minutes. Be sure to keep track of the actual time your student spends on this part of the assessment. You may attempt to clarify the wording of a question if your student does not understand, but you should not answer specific questions asking how to solve a particular problem.
When your student has completed his work on paper, come back to the computer to complete the rest of the assessment.
Instructor Portion:
Use this tool as an opportunity to help you determine your student’s understanding of the concepts.
For each problem, first check to see if the student answered it correctly. Then ask your student to explain to you how he arrived at each of his answers, or “teach back” the solution. Based on your student’s response, choose the statement(s) that most accurately describe how your student solved the problem. (IMPORTANT: Several of the questions require multiple responses. Be sure to mark ALL appropriate responses.)
Quiz-summary
0 of 14 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
Results
Time has elapsed
Categories
- Not categorized 0%
-
Your student’s performance indicates that he would be more successful in a lower level. Here are some additional steps you can take.
-
Your student’s performance indicates that he may be ready for Algebra 2. Here are some additional steps you should take.
-
Your student is ready for Algebra 2. Please be advised, however, that many students complete the Math-U-See Geometry course before moving into Algebra 2. You will see review problems from Geometry on Algebra 2 tests, but you may omit them if your student has not yet covered the material.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- Answered
- Review
- Question 1 of 14
1. Question
CORRECT ANSWER: 7x3
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 7x3
The student was expected to know how to find the square root of an expression. In this case, he needed to find the square root of 49 (7) and the square root of x6 (x3 because x3 ∙ x3 = x6).
SKILL: Simplify a radical expression.
IncorrectCORRECT ANSWER: 7x3
The student was expected to know how to find the square root of an expression. In this case, he needed to find the square root of 49 (7) and the square root of x6 (x3 because x3 ∙ x3 = x6).
SKILL: Simplify a radical expression.
- Question 2 of 14
2. Question
CORRECT ANSWER: x = 180
SAMPLE SOLUTIONS:
Solution 1
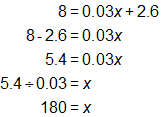
Solution 2
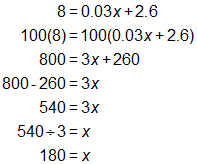
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: x = 180
SAMPLE SOLUTIONS:
SAMPLE SOLUTIONS:Solution 1
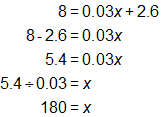
Solution 2
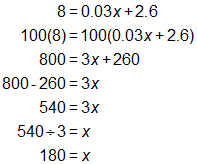
The student needs to be able to solve two-step equations with decimal and fractional values.
SKILL: Solve a two-step equation involving decimal numbers.
IncorrectCORRECT ANSWER: x = 180
SAMPLE SOLUTIONS:
SAMPLE SOLUTIONS:Solution 1
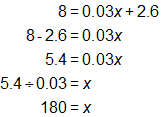
Solution 2
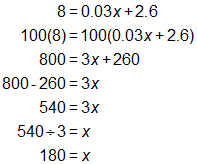
The student needs to be able to solve two-step equations with decimal and fractional values.
SKILL: Solve a two-step equation involving decimal numbers.
- Question 3 of 14
3. Question
CORRECT ANSWER: y = -3x + 2
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: y = -3x + 2
The student needed to use the standard formula for a line, y = mx + b, where m = the slope of the line and b = the y-intercept. He needed to choose any two points on the graph, such as (1, -1) and (0, 2), and either count over and up (as shown here) or subtract the y values and the x values to find the slope:
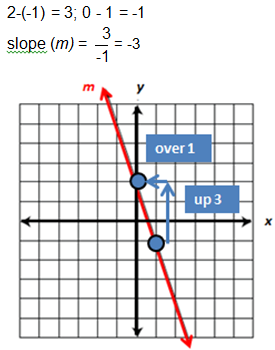
Next, the student needed to find the y-intercept. The graph crosses the y-axis at +2. Substituting the slope and y-intercept into the standard formula, the equation of the graph becomes y = -3x + 2.
SKILL: Write an equation for a graph.
IncorrectCORRECT ANSWER: y = -3x + 2
The student needed to use the standard formula for a line, y = mx + b, where m = the slope of the line and b = the y-intercept. He needed to choose any two points on the graph, such as (1, -1) and (0, 2), and either count over and up (as shown here) or subtract the y values and the x values to find the slope:

Next, the student needed to find the y-intercept. The graph crosses the y-axis at +2. Substituting the slope and y-intercept into the standard formula, the equation of the graph becomes y = -3x + 2.
SKILL: Write an equation for a graph.
- Question 4 of 14
4. Question
CORRECT ANSWER:
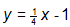
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
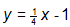
Write the equation of a line that is perpendicular to the graph of the line created by y = -4x
IncorrectCORRECT ANSWER:
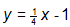
Write the equation of a line that is perpendicular to the graph of the line created by y = -4x
- Question 5 of 14
5. Question
CORRECT ANSWER: x = 5 and y = 3 OR {5, 3}
SAMPLE SOLUTIONS:
Solution 1
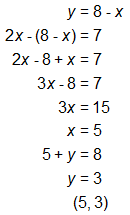
Solution 2
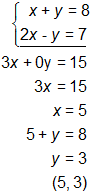
Solution 3
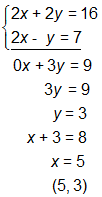
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: x = 5 and y = 3 OR {5, 3}
SAMPLE SOLUTIONS:
Solution 1
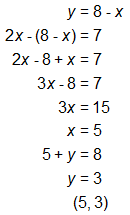
In this solution, the first equation was rewritten to isolate the variable y. The value of y (8 – x) could then be substituted into the second equation to find the value of x (5). Once this step was completed, the value of x was substituted back into the first equation to find the value of y(3).
Solution 2
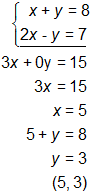
In this solution, the two equations were added together, term by term. The y and –y gave a sum of zero, which enabled the student to find the value of x (5). Once this step was completed, the value of x was substituted back into the first equation to find the value of y (3).
Solution 3
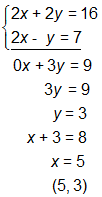
In this solution, each term of the first equation was multiplied by 2. The second equation was subtracted from the first equation, term by term, enabling the student to find the value of y (3). This was substituted back into the first equation to find the value of x (5).
SKILL: Solve a system of linear equations.
IncorrectCORRECT ANSWER: x = 5 and y = 3 OR {5, 3}
SAMPLE SOLUTIONS:
Solution 1
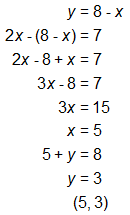
In this solution, the first equation was rewritten to isolate the variable y. The value of y (8 – x) could then be substituted into the second equation to find the value of x (5). Once this step was completed, the value of x was substituted back into the first equation to find the value of y(3).
Solution 2
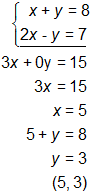
In this solution, the two equations were added together, term by term. The y and –y gave a sum of zero, which enabled the student to find the value of x (5). Once this step was completed, the value of x was substituted back into the first equation to find the value of y (3).
Solution 3
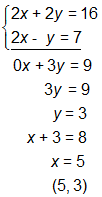
In this solution, each term of the first equation was multiplied by 2. The second equation was subtracted from the first equation, term by term, enabling the student to find the value of y (3). This was substituted back into the first equation to find the value of x (5).
SKILL: Solve a system of linear equations.
- Question 6 of 14
6. Question
CORRECT ANSWER: -10, -8, and -6
SAMPLE SOLUTION:
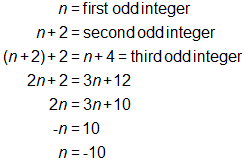
The first odd integer is -10.
The second odd integer is -10 + 2 = -8.
The third odd integer is -10 + 4 = -6.Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: -10, -8, and -6
1) The student should have named the three integers using variables. If the first integer is n, the second must be n + 2 because the integers are odd and therefore two numbers apart. This means the third integer is four numbers apart from the original and can be named as n + 4.
2) The student was expected to write an equation to represent the problem, using these expressions for the integers.
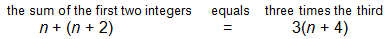
3) The student should then have solved for the variable n.
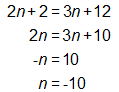
4) The student should have used this information to find the other two integers.
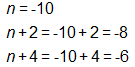
The three integers are -10, -8, and -6.
SKILL: Solve a problem involving consecutive integers.
IncorrectCORRECT ANSWER: -10, -8, and -6
1) The student should have named the three integers using variables. If the first integer is n, the second must be n + 2 because the integers are odd and therefore two numbers apart. This means the third integer is four numbers apart from the original and can be named as n + 4.
2) The student was expected to write an equation to represent the problem, using these expressions for the integers.
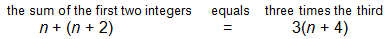
3) The student should then have solved for the variable n.
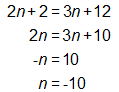
4) The student should have used this information to find the other two integers.
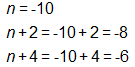
The three integers are -10, -8, and -6.
SKILL: Solve a problem involving consecutive integers.
- Question 7 of 14
7. Question
CORRECT ANSWER: 2x2 – 7x – 15
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 2x2 – 7x – 15
POSSIBLE SOLUTIONS:
1) The student could have used the Distributive Property to multiply each term in the first binomial by the second binomial.
(2x + 3)(x – 5) = 2x(x – 5) + 3 (x – 5) = (2x2 – 10x) + (3x – 15) = 2x2 – 7x – 152) The student could have used the FOIL strategy (multiply first terms together, outer terms, inner terms, and last terms).
(2x + 3)(x – 5) = 2x(x) + 2x(-5) + 3(x) + 3(-5) = 2x2 – 10x + 3x – 15 = 2x2 – 7x – 15SKILL: Multiply binomials.
IncorrectCORRECT ANSWER: 2x2 – 7x – 15
POSSIBLE SOLUTIONS:
1) The student could have used the Distributive Property to multiply each term in the first binomial by the second binomial.
(2x + 3)(x – 5) = 2x(x – 5) + 3 (x – 5) = (2x2 – 10x) + (3x – 15) = 2x2 – 7x – 152) The student could have used the FOIL strategy (multiply first terms together, outer terms, inner terms, and last terms).
(2x + 3)(x – 5) = 2x(x) + 2x(-5) + 3(x) + 3(-5) = 2x2 – 10x + 3x – 15 = 2x2 – 7x – 15SKILL: Multiply binomials.
- Question 8 of 14
8. Question
CORRECT ANSWER: 4(x + 3)(x – 3)
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 4(x + 3)(x – 3)
POSSIBLE SOLUTIONS:
1) Recognize that 4x2 – 36 is the difference of two squares.
4x2 – 36 = (2x + 6)(2x – 6) = 2(x + 3) x 2(x – 3) = 4(x + 3)(x – 3)2) Factor out the greatest common factor (4) and then find the difference between two squares.
4x2 – 36 = 4(x2 – 9) = 4(x + 3)(x – 3)IncorrectCORRECT ANSWER: 4(x + 3)(x – 3)
POSSIBLE SOLUTIONS:
1) Recognize that 4x2 – 36 is the difference of two squares.
4x2 – 36 = (2x + 6)(2x – 6) = 2(x + 3) x 2(x – 3) = 4(x + 3)(x – 3)2) Factor out the greatest common factor (4) and then find the difference between two squares.
4x2 – 36 = 4(x2 – 9) = 4(x + 3)(x – 3) - Question 9 of 14
9. Question
CORRECT ANSWER: x = -3, x = -1 OR x = {-3, -1}
SAMPLE SOLUTIONS:
Solution A
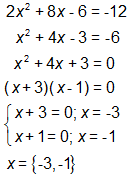
Solution B
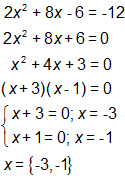
Solution C
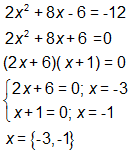
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: x = -3, x = -1 OR x = {-3, -1}
Solution A
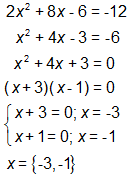
In this solution, the equation was simplified by dividing all terms by the common factor of 2. Then 6 was added to both sides to set the equation equal to zero. The polynomial was factored into two binomials, each of which was set equal to zero. This gave the two possible solutions of -3 and -1.
Solution B
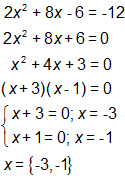
In this solution, 12 was added to both sides to set the equation equal to zero. Then the common factor of 2 was divided out, and the polynomial was factored into two binomials, as in the first solution.
Solution C
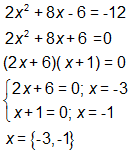
In this solution, 12 was also added to both sides to set the equation equal to zero. Then the resulting polynomial was factored into two binomials. Both were set equal to zero, resulting in the same two solutions: -3 and -1.
SKILL: Factor a polynomial to solve an equation.
IncorrectCORRECT ANSWER: x = -3, x = -1 OR x = {-3, -1}
Solution A
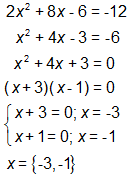
In this solution, the equation was simplified by dividing all terms by the common factor of 2. Then 6 was added to both sides to set the equation equal to zero. The polynomial was factored into two binomials, each of which was set equal to zero. This gave the two possible solutions of -3 and -1.
Solution B
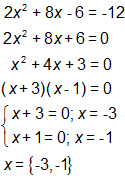
In this solution, 12 was added to both sides to set the equation equal to zero. Then the common factor of 2 was divided out, and the polynomial was factored into two binomials, as in the first solution.
Solution C
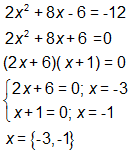
In this solution, 12 was also added to both sides to set the equation equal to zero. Then the resulting polynomial was factored into two binomials. Both were set equal to zero, resulting in the same two solutions: -3 and -1.
SKILL: Factor a polynomial to solve an equation.
- Question 10 of 14
10. Question
CORRECT ANSWER:
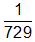
SAMPLE SOLUTIONS:
Solution A
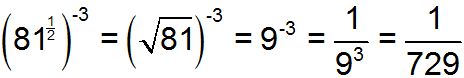
Solution B
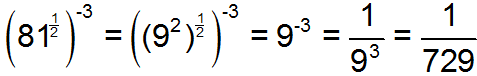
Solution C
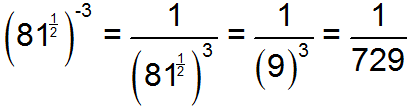
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
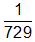
Solution A
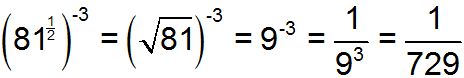
In this solution, the student recognized that
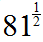 means the square root of 81, which is 9. Then he recognized that a negative exponent meant that he needed to find the inverse of 93 (729).
means the square root of 81, which is 9. Then he recognized that a negative exponent meant that he needed to find the inverse of 93 (729).Solution B
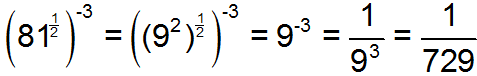
In this solution, the student rewrote 81 as 92. When he raised 92 to the one-half power, he multiplied the exponents, giving 91, or 9. Then he recognized that a negative exponent meant that he needed to find the inverse of 93 (729).
Solution C
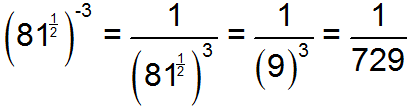
In this solution, the student first rewrote the negative exponent as its inverse. Then he simplified the denominator by finding the square root of 81 (9) and raising it to the third power.
IncorrectCORRECT ANSWER:
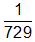
Solution A
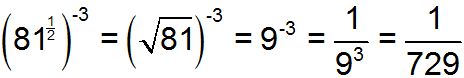
In this solution, the student recognized that
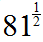 means the square root of 81, which is 9. Then he recognized that a negative exponent meant that he needed to find the inverse of 93 (729).
means the square root of 81, which is 9. Then he recognized that a negative exponent meant that he needed to find the inverse of 93 (729).Solution B
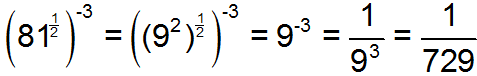
In this solution, the student rewrote 81 as 92. When he raised 92 to the one-half power, he multiplied the exponents, giving 91, or 9. Then he recognized that a negative exponent meant that he needed to find the inverse of 93 (729).
Solution C
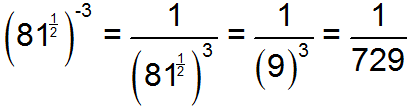
In this solution, the student first rewrote the negative exponent as its inverse. Then he simplified the denominator by finding the square root of 81 (9) and raising it to the third power.
- Question 11 of 14
11. Question
CORRECT ANSWER:

Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:

The student was expected to know the relationship between meters and centimeters: 1 m = 100 cm. Since the measurement being changed is in meters, the ratio needs to have meters underneath in order to cancel out the unit. If the student had been asked to complete the calculation, the solution would have looked like this:
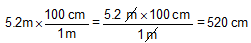
SKILL: Use a unit multiplier to convert measurements.
IncorrectCORRECT ANSWER:

The student was expected to know the relationship between meters and centimeters: 1 m = 100 cm. Since the measurement being changed is in meters, the ratio needs to have meters underneath in order to cancel out the unit. If the student had been asked to complete the calculation, the solution would have looked like this:
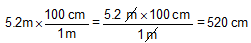
SKILL: Use a unit multiplier to convert measurements.
- Question 12 of 14
12. Question
CORRECT ANSWER: 2.5 x 10-4
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 2.5 x 10-4
In order to solve this problem, the student needed to understand that scientific notation is a rewriting of a number in exponential notation, using the place value of the first nonzero digit. In this case, the first nonzero digit is 2, and it is in the ten-thousandths place. In other words, the number could be rewritten as follows:
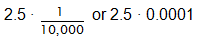
Since the power of ten is shown as a fraction or decimal, the exponent must be negative, which means it would be rewritten as 10-4.
SKILL: Write a number in scientific notation.
IncorrectCORRECT ANSWER: 2.5 x 10-4
In order to solve this problem, the student needed to understand that scientific notation is a rewriting of a number in exponential notation, using the place value of the first nonzero digit. In this case, the first nonzero digit is 2, and it is in the ten-thousandths place. In other words, the number could be rewritten as follows:
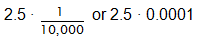
Since the power of ten is shown as a fraction or decimal, the exponent must be negative, which means it would be rewritten as 10-4.
SKILL: Write a number in scientific notation.
- Question 13 of 14
13. Question
The next two questions are just for the instructor to complete. Click on the statement that best describes your student’s work during the written part of the assessment.
How long did it take the student to complete the written part of the assessment? Click on the best response.
CorrectA student who has mastered the prerequisite concepts should be able to complete the written assessment in about 45 minutes.
IncorrectA student who has mastered the prerequisite concepts should be able to complete the written assessment in about 45 minutes.
- Question 14 of 14
14. Question
How often did the student ask for help or hints as to how to solve a problem? (This is different than asking for clarification about how a question is worded.) Click on the best response.
CorrectA student who has mastered the prerequisite concepts should feel confident in his or her ability to solve the problems and should not need to ask for assistance.
IncorrectA student who has mastered the prerequisite concepts should feel confident in his or her ability to solve the problems and should not need to ask for assistance.