Introduction:
Students who are ready for Calculus have successfully completed Algebra 1, Algebra 2, Geometry, and PreCalculus (Trigonometry/Advanced Math). If you are unsure whether your student is ready for Calculus, or if you are new to Math-U-See, we strongly encourage you to complete the following assessment with the student.
Preparing for the Assessment:
You will need the following items:
- pencil with eraser
- extra paper for calculation, if desired
Students may also use a calculator to complete this assessment.
Gather these materials before you begin.
Student Portion:
Print out a copy of the Calculus Readiness Assessment. The printed part of the assessment is to be completed independently by the student and should take approximately 45 minutes. Be sure to keep track of the actual time your student spends on this part of the assessment. You may attempt to clarify the wording of a question if your student does not understand, but you should not answer specific questions asking how to solve a particular problem.
When your student has completed his work on paper, come back to the computer to complete the rest of the assessment.
Instructor Portion:
Use this tool as an opportunity to help you determine your student’s understanding of the concepts.
For each problem, first check to see if the student answered it correctly. Then ask your student to explain to you how he arrived at each of his answers, or “teach back” the solution. Based on your student’s response, choose the statement(s) that most accurately describe how your student solved the problem. (IMPORTANT: Several of the questions require multiple responses. Be sure to mark ALL appropriate responses.)
Quiz-summary
0 of 17 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
Results
Time has elapsed
Categories
- Not categorized 0%
-
Your student’s performance indicates that he would be more successful in a lower level. Here are some additional steps you can take.
-
Your student’s performance indicates that he may be ready for Calculus. Here are some additional steps you should take.
-
Your student is ready for Calculus.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- Answered
- Review
- Question 1 of 17
1. Question
CORRECT ANSWERS:
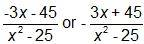
SAMPLE SOLUTION:
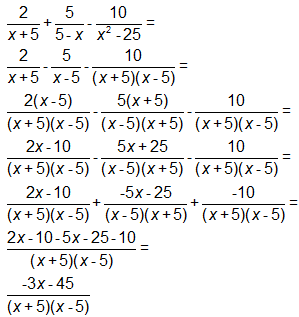
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWERS:
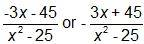
SAMPLE SOLUTION:
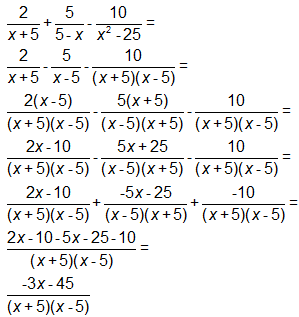
At this level, students are expected to be skilled at simplifying rational expressions. For this particular problem, the student needed to have mastered the following concepts:
1) Factor the difference of two squares
2) Identify the effect of a negative sign on an entire expression
3) Rename rational expressions so that they have a common denominator
4) Simplify expressions by combining like termsSKILL: Simplify a rational expression.
IncorrectCORRECT ANSWERS:
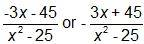
SAMPLE SOLUTION:
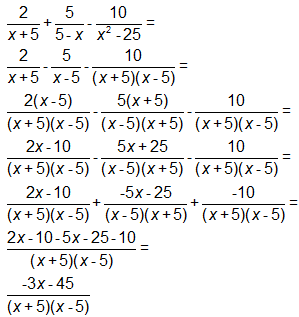
At this level, students are expected to be skilled at simplifying rational expressions. For this particular problem, the student needed to have mastered the following concepts:
1) Factor the difference of two squares
2) Identify the effect of a negative sign on an entire expression
3) Rename rational expressions so that they have a common denominator
4) Simplify expressions by combining like termsSKILL: Simplify a rational expression.
- Question 2 of 17
2. Question
SAMPLE ANSWERS: The graph of 2x2 is narrower than the graph of x2.
The graph of x2 is wider than the graph of 2x2.Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectSAMPLE ANSWERS: The graph of 2x2 is narrower than the graph of x2.
The graph of x2 is wider than the graph of 2x2.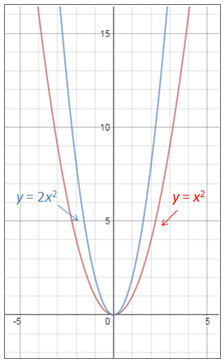
Ideally, the student should have been familiar with the standard equation of a parabola (y = x2) and should not have needed to graph the equations. He should have known that adding a coefficient of 2 to the term x2 would make the graph narrower.
SKILL: Identify the effect of the coefficient on the graph of a second-degree equation.
IncorrectSAMPLE ANSWERS: The graph of 2x2 is narrower than the graph of x2.
The graph of x2 is wider than the graph of 2x2.
Ideally, the student should have been familiar with the standard equation of a parabola (y = x2) and should not have needed to graph the equations. He should have known that adding a coefficient of 2 to the term x2 would make the graph narrower.
SKILL: Identify the effect of the coefficient on the graph of a second-degree equation.
- Question 3 of 17
3. Question
CORRECT ANSWER: The x and y axes are the asymptotes.
Ask the student to explain how he found his answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: The x and y axes are the asymptotes.
The student needed to know that an asymptote is a line that a graph approaches but never meets. In this case, both parts of the graph come close to both the x axis and y axis but will never meet them. This is because x and y will never equal zero.
SKILL: Identify the asymptote(s) for a hyperbola.
IncorrectCORRECT ANSWER: The x and y axes are the asymptotes.
The student needed to know that an asymptote is a line that a graph approaches but never meets. In this case, both parts of the graph come close to both the x axis and y axis but will never meet them. This is because x and y will never equal zero.
SKILL: Identify the asymptote(s) for a hyperbola.
- Question 4 of 17
4. Question
CORRECT ANSWER: (-3, 8)
SAMPLE SOLUTIONS:
Solution A:
Compare the equation to the standard form of a quadratic: y = ax2 + bx + c.
For this equation, a = 1, b = -6, and c = 1.
The x value of the vertex is found by using the formula: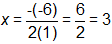
Substitute this value into the equation to find the value of y.
y = (3)2 – 6(3) + 1 = 9 – 18 + 1 = -8
The vertex is located at (3, -8).Solution B:
Complete the square to rewrite the equation in vertex form of a quadratic: y = a(x – h)2 + k. In this case, something must be added to x2 – 6x to make it the perfect square of a binomial. You can add the zero pair of 9 and -9 to accomplish this purpose.
y = x2 – 6x + 1
y = (x2 – 6x + 1) + (9 – 9)
y = (x2 – 6x + 9+ (1 – 9)
y = (x– 3)2 – 8
The vertex is located at (h, k), or, in this case, (3, -8).Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: (-3, 8)
The student should have worked through either of the following solutions to find the vertex (in this case, the lowest point of the parabola).
SAMPLE SOLUTIONS:
Solution A:
Compare the equation to the standard form of a quadratic: y = ax2 + bx + c.
For this equation, a = 1, b = -6, and c = 1.
The x value of the vertex is found by using the formula: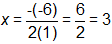
Substitute this value into the equation to find the value of y.
y = (3)2 – 6(3) + 1 = 9 – 18 + 1 = -8
The vertex is located at (3, -8).Solution B:
Complete the square to rewrite the equation in vertex form of a quadratic: y = a(x – h)2 + k. In this case, something must be added to x2 – 6x to make it the perfect square of a binomial. You can add the zero pair of 9 and -9 to accomplish this purpose.
y = x2 – 6x + 1
y = (x2 – 6x + 1) + (9 – 9)
y = (x2 – 6x + 9+ (1 – 9)
y = (x– 3)2 – 8
The vertex is located at (h, k), or, in this case, (3, -8).SKILL: Identify the vertex of a quadratic.
IncorrectCORRECT ANSWER: (-3, 8)
The student should have worked through either of the following solutions to find the vertex (in this case, the lowest point of the parabola).
SAMPLE SOLUTIONS:
Solution A:
Compare the equation to the standard form of a quadratic: y = ax2 + bx + c.
For this equation, a = 1, b = -6, and c = 1.
The x value of the vertex is found by using the formula: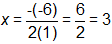
Substitute this value into the equation to find the value of y.
y = (3)2 – 6(3) + 1 = 9 – 18 + 1 = -8
The vertex is located at (3, -8).Solution B:
Complete the square to rewrite the equation in vertex form of a quadratic: y = a(x – h)2 + k. In this case, something must be added to x2 – 6x to make it the perfect square of a binomial. You can add the zero pair of 9 and -9 to accomplish this purpose.
y = x2 – 6x + 1
y = (x2 – 6x + 1) + (9 – 9)
y = (x2 – 6x + 9+ (1 – 9)
y = (x– 3)2 – 8
The vertex is located at (h, k), or, in this case, (3, -8).SKILL: Identify the vertex of a quadratic.
- Question 5 of 17
5. Question
CORRECT ANSWER:

Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:

First, the student needed to identify the 4-meter side of the triangle as the opposite side, the 3-meter side as the adjacent side, and/or the 5-meter side as the hypotenuse. Then he should have known that the secant is the reciprocal (inverse, or opposite) of the cosine, or the ratio of the measures of the hypotenuse and the adjacent side in the triangle. This ratio is 5/3, which can be calculated as 1.6667 or 1.6666, with the 6 repeating.
SKILL: Identify the reciprocals of the basic trigonometric functions.
IncorrectCORRECT ANSWER:

First, the student needed to identify the 4-meter side of the triangle as the opposite side, the 3-meter side as the adjacent side, and/or the 5-meter side as the hypotenuse. Then he should have known that the secant is the reciprocal (inverse, or opposite) of the cosine, or the ratio of the measures of the hypotenuse and the adjacent side in the triangle. This ratio is 5/3, which can be calculated as 1.6667 or 1.6666, with the 6 repeating.
SKILL: Identify the reciprocals of the basic trigonometric functions.
- Question 6 of 17
6. Question
CORRECT ANSWER: 40 degrees
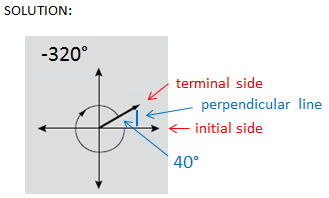
The x-axis is the initial side of the angle.
The negative sign indicates that the terminal side is located 320 degrees clockwise from the initial side.
To find the reference angle, draw a perpendicular line from the terminal side to the x-axis.
The measure of that angle is 40 degrees.Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 40 degrees

The student should have begun at the x-axis and moved 320 degrees clockwise because the sign is negative.
From there, the student should have drawn a perpendicular line from the terminal side to the x-axis.
The measure of that angle is 40 degrees.SKILL: Find the reference angle for any given angle.
IncorrectCORRECT ANSWER: 40 degrees

The student should have begun at the x-axis and moved 320 degrees clockwise because the sign is negative.
From there, the student should have drawn a perpendicular line from the terminal side to the x-axis.
The measure of that angle is 40 degrees.SKILL: Find the reference angle for any given angle.
- Question 7 of 17
7. Question
CORRECT ANSWER:
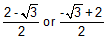
SAMPLE SOLUTION:
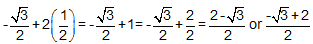
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
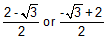
SAMPLE SOLUTION:
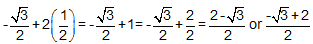
The student should know the values for common trigonometric ratios. In this case, he should have known that the sine of 240 degrees is
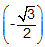 and the cosine of 300 degrees is
and the cosine of 300 degrees is 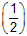 . He would then insert this information into the expression and simply accordingly.
. He would then insert this information into the expression and simply accordingly.SKILL: Identify the ratios for common trigonometric functions.
IncorrectCORRECT ANSWER:
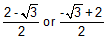
SAMPLE SOLUTION:
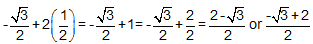
The student should know the values for common trigonometric ratios. In this case, he should have known that the sine of 240 degrees is
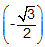 and the cosine of 300 degrees is
and the cosine of 300 degrees is 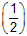 . He would then insert this information into the expression and simply accordingly.
. He would then insert this information into the expression and simply accordingly.SKILL: Identify the ratios for common trigonometric functions.
- Question 8 of 17
8. Question
CORRECT ANSWERS:
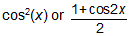
SOLUTIONS:
Solution A:
Use the identity sin2(x) + cos2(x) = 1. Rewrite it as 1 – sin2(x) = cos2(x).Solution A:
Use the double-angle identity: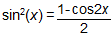
Substitute this into the expression 1 – sin2(x) as follows:
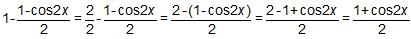
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWERS:
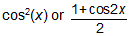
The student should know the basic trigonometric identity, sin2(x) + cos2(x) = 1. This would have enabled him to rewrite the expression as 1 – sin2(x) = cos2(x). Some students may also be able to recall the double-angle identity:
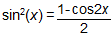 . This could be substituted into the expression 1 – sin2(x) as follows:
. This could be substituted into the expression 1 – sin2(x) as follows:
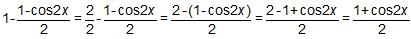
SKILL: Identify the basic trigonometric identities.
IncorrectCORRECT ANSWERS:
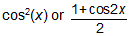
The student should know the basic trigonometric identity, sin2(x) + cos2(x) = 1. This would have enabled him to rewrite the expression as 1 – sin2(x) = cos2(x). Some students may also be able to recall the double-angle identity:
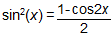 . This could be substituted into the expression 1 – sin2(x) as follows:
. This could be substituted into the expression 1 – sin2(x) as follows:
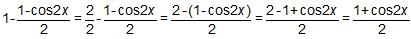
SKILL: Identify the basic trigonometric identities.
- Question 9 of 17
9. Question
CORRECT ANSWER:
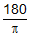
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
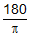
The student should know the relationship between degrees and radians and should be able to convert one to the other.
SKILL: Convert between degrees and radians.
IncorrectCORRECT ANSWER:
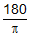
The student should know the relationship between degrees and radians and should be able to convert one to the other.
SKILL: Convert between degrees and radians.
- Question 10 of 17
10. Question
CORRECT ANSWERS:
The range includes all values greater than or equal to 0.
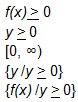
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWERS:
The range includes all values greater than or equal to 0.
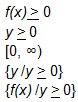
The student should know that the range refers to all possible values for f(x). In this case, because the function involves a radical, the value of the expression inside the radical (x + 3) can never be less than zero. This information can be presented in any of the ways shown as correct answers. (Note: the student may not have read carefully and may have identified the domain (all possible values of x) as all numbers greater than or equal to -3.)
SKILL: Identify the range of a function.
IncorrectCORRECT ANSWERS:
The range includes all values greater than or equal to 0.
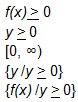
The student should know that the range refers to all possible values for f(x). In this case, because the function involves a radical, the value of the expression inside the radical (x + 3) can never be less than zero. This information can be presented in any of the ways shown as correct answers. (Note: the student may not have read carefully and may have identified the domain (all possible values of x) as all numbers greater than or equal to -3.)
SKILL: Identify the range of a function.
- Question 11 of 17
11. Question
CORRECT ANSWERS:
(2x + 3)2
(2x + 3)(2x + 3)
4x2 + 12x + 9Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWERS:
(2x + 3)2
(2x + 3)(2x + 3)
4x2 + 12x + 9The student should have seen that he needed to substitute the entire expression for f(x), 2x + 3, into the g(x) function, x2. This would have given any of the correct answers shown.
SKILL: Evaluate composite functions.
IncorrectCORRECT ANSWERS:
(2x + 3)2
(2x + 3)(2x + 3)
4x2 + 12x + 9The student should have seen that he needed to substitute the entire expression for f(x), 2x + 3, into the g(x) function, x2. This would have given any of the correct answers shown.
SKILL: Evaluate composite functions.
- Question 12 of 17
12. Question
CORRECT ANSWERS: x = 1; x = {1}
SAMPLE SOLUTION:
log2x + log2(x + 3) = 2
log2x(x + 3) = 2
x(x + 3) = 22
x2 + 3x = 4
x2 + 3x – 4 = 0
(x + 4)(x – 1) = 0
x + 4 = 0 or x – 1 = 0
x = -4 or x = 1
However, x cannot be a negative number, so the only valid solution is x = 1 or x = {1}.Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWERS: x = 1; x = {1}
The student should be familiar with logarithms and know how to manipulate them. In this case, because both logarithms have a base of 2, they can be combined by multiplication. The student should also have known that a logarithm with a base of 2 can be renamed as an exponent of 2, which would have enabled the student to solve as follows:
log2x + log2(x + 3) = 2
log2x(x + 3) = 2
x(x + 3) = 22
x2 + 3x = 4
x2 + 3x – 4 = 0
(x + 4)(x – 1) = 0
x + 4 = 0 or x – 1 = 0
x = -4 or x = 1
However, x cannot be a negative number, so the only valid solution is x = 1 or x = {1}.SKILL: Simplify logarithmic expressions.
IncorrectCORRECT ANSWERS: x = 1; x = {1}
The student should be familiar with logarithms and know how to manipulate them. In this case, because both logarithms have a base of 2, they can be combined by multiplication. The student should also have known that a logarithm with a base of 2 can be renamed as an exponent of 2, which would have enabled the student to solve as follows:
log2x + log2(x + 3) = 2
log2x(x + 3) = 2
x(x + 3) = 22
x2 + 3x = 4
x2 + 3x – 4 = 0
(x + 4)(x – 1) = 0
x + 4 = 0 or x – 1 = 0
x = -4 or x = 1
However, x cannot be a negative number, so the only valid solution is x = 1 or x = {1}.SKILL: Simplify logarithmic expressions.
- Question 13 of 17
13. Question
CORRECT ANSWER:0.8047 (If the student did not have access to a calculator, accept
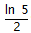 .)
.)SAMPLE SOLUTION:
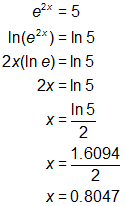
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:0,8047 (If the student did not have access to a calculator, accept
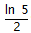 .)
.)The student should be familiar with natural exponential and logarithmic functions and be able to manipulate them. This would have enabled him to solve the equation as follows:
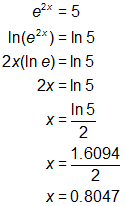
SKILL: Solve exponential equations.
IncorrectCORRECT ANSWER:0,8047 (If the student did not have access to a calculator, accept
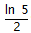 .)
.)The student should be familiar with natural exponential and logarithmic functions and be able to manipulate them. This would have enabled him to solve the equation as follows:
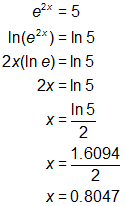
SKILL: Solve exponential equations.
- Question 14 of 17
14. Question
SAMPLE ANSWERS: (Accept either or both):

Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectSAMPLE ANSWERS: (Accept either or both):

The student needed to be familiar with the parent graphs for the basic trigonometric functions– in this case, the sine function. The student should have identified the two differences between the equations and interpreted how they would affect the graph. The sine graph normally has a period of 2 times pi, which would be reduced by half because of the coefficient of 2 in the other equation. Also, subtracting pi/4 would move the graph of the sine function to the right by that amount.
SKILL: Identify how the characteristics of an equation affect the standard graph of a trigonometric function.
IncorrectSAMPLE ANSWERS: (Accept either or both):

The student needed to be familiar with the parent graphs for the basic trigonometric functions– in this case, the sine function. The student should have identified the two differences between the equations and interpreted how they would affect the graph. The sine graph normally has a period of 2 times pi, which would be reduced by half because of the coefficient of 2 in the other equation. Also, subtracting pi/4 would move the graph of the sine function to the right by that amount.
SKILL: Identify how the characteristics of an equation affect the standard graph of a trigonometric function.
- Question 15 of 17
15. Question
CORRECT ANSWER: -4
SAMPLE SOLUTION:
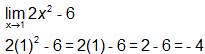
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: -4
The student should have been able to evaluate the limit as follows:
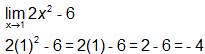
SKILL: Evaluate a limit.
IncorrectCORRECT ANSWER: -4
The student should have been able to evaluate the limit as follows:
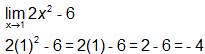
SKILL: Evaluate a limit.
- Question 16 of 17
16. Question
How long did it take the student to complete the assessment? Click on the best response.
CorrectA student who has mastered the prerequisite concepts should be able to complete the written assessment in about 45 minutes.
IncorrectA student who has mastered the prerequisite concepts should be able to complete the written assessment in about 45 minutes.
- Question 17 of 17
17. Question
How often did the student ask for help or hints as to how to solve a problem? (Note: this is different than asking for clarification about how a question is worded.) Click on the best response.
CorrectA student who has mastered the prerequisite concepts should feel confident in his or her ability to solve the problems and should not need to ask for assistance.
IncorrectA student who has mastered the prerequisite concepts should feel confident in his or her ability to solve the problems and should not need to ask for assistance.