Introduction:
Students who are ready for PreCalculus have successfully completed Algebra 1, Geometry, and Algebra 2.Preparing for the Assessment:
You will need the following items:
- paper
- pencil with eraser
Students may also use a calculator to complete this assessment.
Gather these materials before you begin.
Student Portion:
Print out a copy of the PreCalculus Readiness Assessment. The printed part of the assessment is to be completed independently by the student and should take approximately 45 minutes. Be sure to keep track of the actual time your student spends on this part of the assessment. You may attempt to clarify the wording of a question if your student does not understand, but you should not answer specific questions asking how to solve a particular problem.
When your student has completed his work on paper, come back to the computer to complete the rest of the assessment.
Instructor Portion:
Use this tool as an opportunity to help you determine your student’s understanding of the concepts.
For each problem, first check to see if the student answered it correctly. Then ask your student to explain to you how he arrived at each of his answers, or “teach back” the solution. Based on your student’s response, choose the statement(s) that most accurately describe how your student solved the problem. (IMPORTANT: Several of the questions require multiple responses. Be sure to mark ALL appropriate responses.)
Quiz-summary
0 of 17 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
Information
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading…
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Results
Results
Time has elapsed
Categories
- Not categorized 0%
-
Your student’s performance indicates that he would be more successful in a lower level. Here are some additional steps you can take.
-
Your student’s performance indicates that he may be ready for PreCalculus. Here are some additional steps you should take.
-
Your student is ready for PreCalculus.
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- Answered
- Review
- Question 1 of 17
1. Question
CORRECT ANSWER: 15 meters (m)
SAMPLE SOLUTION:
a2 + b2 =c3
x2 + 82 = 172
x2 + 64 = 289
x2 = 289 – 64
x2 = 225
x = 15
The missing side is 15 meters long.
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 15 meters (m)
The student was expected to know and use the Pythagorean Theorem to find the missing side of the triangle.
a2 + b2 =c3
x2 + 82 = 172
x2 + 64 = 289
x2 = 289 – 64
x2 = 225
x = 15
The missing side is 15 meters long.
SKILL: Use the Pythagorean Theorem to find the missing side of a right triangle.
IncorrectCORRECT ANSWER: 15 meters (m)
The student was expected to know and use the Pythagorean Theorem to find the missing side of the triangle.
a2 + b2 =c3
x2 + 82 = 172
x2 + 64 = 289
x2 = 289 – 64
x2 = 225
x = 15
The missing side is 15 meters long.
SKILL: Use the Pythagorean Theorem to find the missing side of a right triangle.
- Question 2 of 17
2. Question
CORRECT ANSWER: x = -43
SAMPLE SOLUTIONS:
Solution A
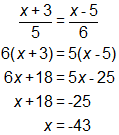
Solution B
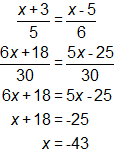
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: x = -43
The student was expected to use knowledge of proportions and solving equations to find the value of x. The sample solutions show two possible ways to solve this problem:
Solution A:
- Cross multiply to solve the proportion.
- Solve the equation by isolating the variable on one side.
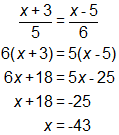
Solution B:
- Rewrite the two fractions with common denominators.
- Set the numerators equal to one another.
- Solve the equation by isolating the variable on one side.
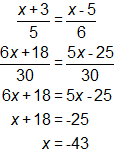
SKILLS: Use ratios to solve real-world problems; solve equations with variables on both sides.
IncorrectCORRECT ANSWER: x = -43
The student was expected to use knowledge of proportions and solving equations to find the value of x. The sample solutions show two possible ways to solve this problem:
Solution A:
- Cross multiply to solve the proportion.
- Solve the equation by isolating the variable on one side.
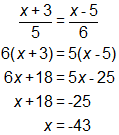
Solution B:
- Rewrite the two fractions with common denominators.
- Set the numerators equal to one another.
- Solve the equation by isolating the variable on one side.
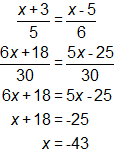
SKILLS: Use ratios to solve real-world problems; solve equations with variables on both sides.
- Question 3 of 17
3. Question
CORRECT ANSWERS:
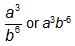
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWERS:
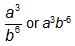
In order to solve this problem, the student needs to have mastered several concepts:
- A fraction can be rewritten as a division problem.

- Division by an exponent can be rewritten as multiplication by its opposite.
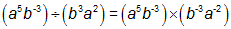
- Only the same variables can be multiplied together.
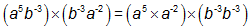
- When variables are multiplied, they can be combined by adding the exponents.
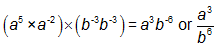
SKILL: Simplify a rational expression.
IncorrectCORRECT ANSWERS:
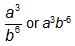
In order to solve this problem, the student needs to have mastered several concepts:
- A fraction can be rewritten as a division problem.

- Division by an exponent can be rewritten as multiplication by its opposite.
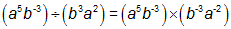
- Only the same variables can be multiplied together.
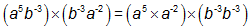
- When variables are multiplied, they can be combined by adding the exponents.
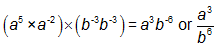
SKILL: Simplify a rational expression.
- Question 4 of 17
4. Question
CORRECT ANSWER: 8qr – r
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 8qr – r
In order to solve this problem, the student needs to have mastered several concepts:
- Variables being multiplied within a term can be combined by adding the exponents.
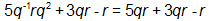
- Terms with the exact same variables can be added or subtracted.
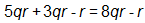
SKILL: Add and subtract to simplify a rational expression.
IncorrectCORRECT ANSWER: 8qr – r
In order to solve this problem, the student needs to have mastered several concepts:
- Variables being multiplied within a term can be combined by adding the exponents.
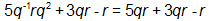
- Terms with the exact same variables can be added or subtracted.
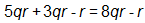
SKILL: Add and subtract to simplify a rational expression.
- Question 5 of 17
5. Question
CORRECT ANSWER:
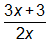
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
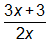
In order to solve this problem, the student needs to have mastered several concepts:
- A fraction can be rewritten as a division problem.

- Division can be rewritten as multiplication by the opposite.
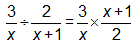
- To multiply fractions, multiply the numerators together and the denominators together.
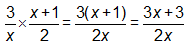
SKILL: Simplify a complex fraction.
IncorrectCORRECT ANSWER:
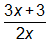
In order to solve this problem, the student needs to have mastered several concepts:
- A fraction can be rewritten as a division problem.

- Division can be rewritten as multiplication by the opposite.
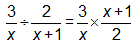
- To multiply fractions, multiply the numerators together and the denominators together.
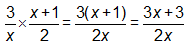
SKILL: Simplify a complex fraction.
- Question 6 of 17
6. Question
CORRECT ANSWER:
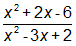
SAMPLE SOLUTION:
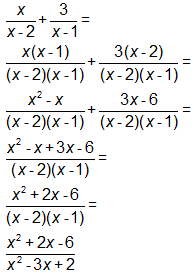
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
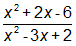
In order to solve this problem, the student needed to know the following concepts:
- Fractions need to have common denominators before they can be combined. The first fraction needed to be multiplied by
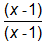 , and the second fraction needed to be multiplied by
, and the second fraction needed to be multiplied by 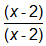 .
.
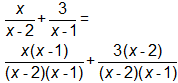
- The Distributive Property needed to be used to create new numerators.
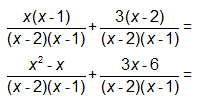
- The numerators needed to be combined over the new denominator, and both numerator and denominator needed to be simplified.
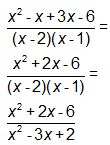
SKILL: Add fractions with polynomials in the denominator.
IncorrectCORRECT ANSWER:
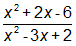
In order to solve this problem, the student needed to know the following concepts:
- Fractions need to have common denominators before they can be combined. The first fraction needed to be multiplied by
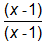 , and the second fraction needed to be multiplied by
, and the second fraction needed to be multiplied by 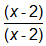 .
.
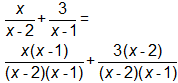
- The Distributive Property needed to be used to create new numerators.
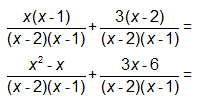
- The numerators needed to be combined over the new denominator, and both numerator and denominator needed to be simplified.
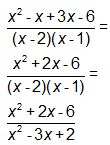
SKILL: Add fractions with polynomials in the denominator.
- Question 7 of 17
7. Question
CORRECT ANSWER:
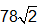
SAMPLE SOLUTIONS:
Solution A
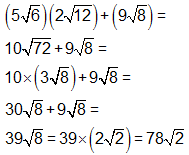
Solution B
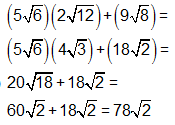
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
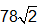
The student needed to understand how to perform operations with radicals. The sample solutions show two ways in which these concepts could be applied:
Solution A:
Here the radicals are combined first and then simplified.
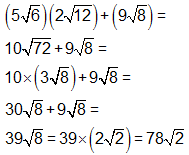
Solution B:Here the radicals are simplified first and then combined.
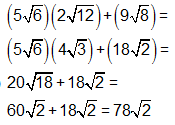
SKILL: Simplify expressions with radicals.
IncorrectCORRECT ANSWER:
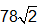
The student needed to understand how to perform operations with radicals. The sample solutions show two ways in which these concepts could be applied:
Solution A:
Here the radicals are combined first and then simplified.
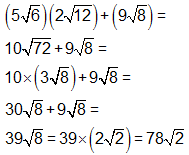
Solution B:Here the radicals are simplified first and then combined.
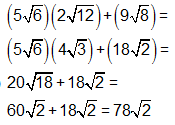
SKILL: Simplify expressions with radicals.
- Question 8 of 17
8. Question
CORRECT ANSWER:
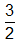
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
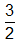
In order to solve this problem, the student needs to have mastered several concepts:
- A negative exponent indicates the reciprocal of the base.
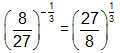
- A fractional exponent indicates a root. In this case, the exponent means the cube root of the base.
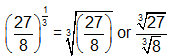
- The cube root is a number that it is multiplied by itself three times to obtain the given number. In this case, 3 ∙ 3 ∙ 3 = 27, and 2 ∙ 2 ∙ 2 = 8.
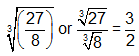
SKILL: Simplify an expression with a fractional exponent.
IncorrectCORRECT ANSWER:
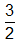
In order to solve this problem, the student needs to have mastered several concepts:
- A negative exponent indicates the reciprocal of the base.
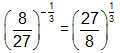
- A fractional exponent indicates a root. In this case, the exponent means the cube root of the base.
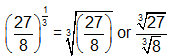
- The cube root is a number that it is multiplied by itself three times to obtain the given number. In this case, 3 ∙ 3 ∙ 3 = 27, and 2 ∙ 2 ∙ 2 = 8.
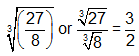
SKILL: Simplify an expression with a fractional exponent.
- Question 9 of 17
9. Question
CORRECT ANSWER: 4
SAMPLE SOLUTIONS:
Solution A
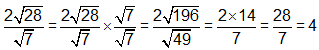
Solution B
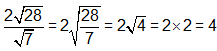
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: 4
SAMPLE SOLUTIONS:
Solution A
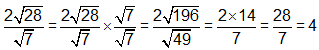
Solution B
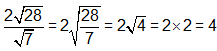
SKILL: Simplify a division expression with irrational numbers.
IncorrectCORRECT ANSWER: 4
SAMPLE SOLUTIONS:
Solution A
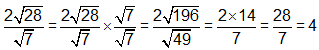
Solution B
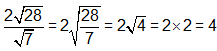
SKILL: Simplify a division expression with irrational numbers.
- Question 10 of 17
10. Question
CORRECT ANSWER: (x3 + 4b)(x3 – 4b)
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: (x3 + 4b)(x3 – 4b)
The student should have recognized the expression as the difference of two squares and factored it accordingly.
SKILL: Factor the difference of two squares.
IncorrectCORRECT ANSWER: (x3 + 4b)(x3 – 4b)
The student should have recognized the expression as the difference of two squares and factored it accordingly.
SKILL: Factor the difference of two squares.
- Question 11 of 17
11. Question
CORRECT ANSWER: -72
SAMPLE SOLUTION:
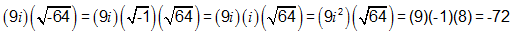
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: -72
The student needed to know that i is an imaginary number representing the square root of -1. He then needed to apply this information to rename square roots of negative numbers and simplify expressions, as follows:
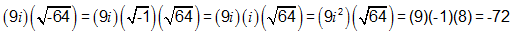
SKILL: Simplify expressions with imaginary numbers.
IncorrectCORRECT ANSWER: -72
The student needed to know that i is an imaginary number representing the square root of -1. He then needed to apply this information to rename square roots of negative numbers and simplify expressions, as follows:
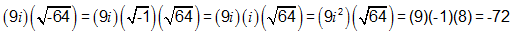
SKILL: Simplify expressions with imaginary numbers.
- Question 12 of 17
12. Question
CORRECT ANSWER:
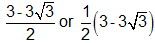
SAMPLE SOLUTION:
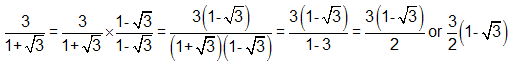
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:
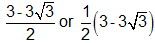
The student was expected to know that he needed to multiply the denominator by the conjugate (
 ) in order to complete the square and obtain a whole-number denominator.
) in order to complete the square and obtain a whole-number denominator.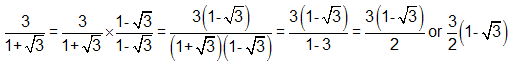
SKILL: Rationalize the denominator of a fraction.
IncorrectCORRECT ANSWER:
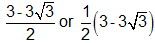
The student was expected to know that he needed to multiply the denominator by the conjugate (
 ) in order to complete the square and obtain a whole-number denominator.
) in order to complete the square and obtain a whole-number denominator.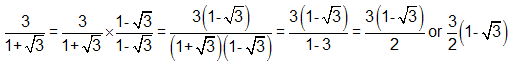
SKILL: Rationalize the denominator of a fraction.
- Question 13 of 17
13. Question
CORRECT ANSWERS:
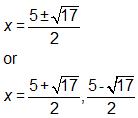
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWERS:
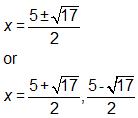
The student was expected to notice that the equation could not be solved by factoring; therefore, he needed to know and use the quadratic formula to find the solution.
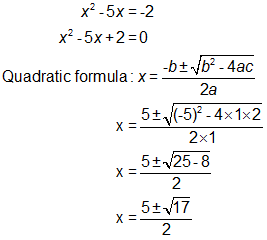 Incorrect
IncorrectCORRECT ANSWERS:
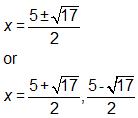
The student was expected to notice that the equation could not be solved by factoring; therefore, he needed to know and use the quadratic formula to find the solution.
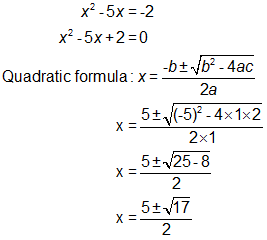
- Question 14 of 17
14. Question
CORRECT ANSWER: E; x2 + y2 = 16
Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER: E; x2 + y2 = 16
The student was expected to know the general equation for a circle: (x−h)2+(y−k)2= r2
The student should also know the general equations for the other answer choices:
A. y = 3x This is the general equation of a line: y = mx + b
This equation can be rewritten as: y = 3x + 0B. y2 = 4x2 – 12 This is the general equation of a hyperbola: x2
IncorrectCORRECT ANSWER: E; x2 + y2 = 16
The student was expected to know the general equation for a circle: (x−h)2+(y−k)2= r2
The student should also know the general equations for the other answer choices:
A. y = 3x This is the general equation of a line: y = mx + b
This equation can be rewritten as: y = 3x + 0B. y2 = 4x2 – 12 This is the general equation of a hyperbola: x2
- Question 15 of 17
15. Question
CORRECT ANSWER:

Ask the student to explain how he found the answer. Which of the following statements characterized his response? CLICK ALL THAT APPLY.
CorrectCORRECT ANSWER:

SKILL: Use unit multipliers (dimensional analysis) to convert units.
IncorrectCORRECT ANSWER:

SKILL: Use unit multipliers (dimensional analysis) to convert units.
- Question 16 of 17
16. Question
The next two questions are for the instructor. Click on the statement that best describes your student’s work during the written part of the assessment.
How long did it take the student to complete the assessment? Click on the best response.
CorrectA student who has mastered the prerequisite concepts should be able to complete the written assessment in about 45 minutes.
IncorrectA student who has mastered the prerequisite concepts should be able to complete the written assessment in about 45 minutes.
- Question 17 of 17
17. Question
How often did the student ask for help or hints as to how to solve a problem? (This is different than asking for clarification about how a question is worded.) Click on the best response.
CorrectA student who has mastered the prerequisite concepts should feel confident in his or her ability to solve the problems and should not need to ask for assistance.
IncorrectA student who has mastered the prerequisite concepts should feel confident in his or her ability to solve the problems and should not need to ask for assistance.